Form-based signatures across GB¶
This notebook explores creation of signatures based on form data only.
The method mirrors creation of standard spatial signatures.
import dask.dataframe
import numpy as np
import pandas as pd
from sklearn.cluster import MiniBatchKMeans
from clustergram import Clustergram
data = dask.dataframe.read_parquet("../../urbangrammar_samba/spatial_signatures/clustering_data/form/standardized/").set_index('hindex')
%time data = data.compute()
data
CPU times: user 51.2 s, sys: 40.2 s, total: 1min 31s
Wall time: 1min 49s
| sdbAre_q1 | sdbAre_q2 | sdbAre_q3 | sdbPer_q1 | sdbPer_q2 | sdbPer_q3 | sdbCoA_q1 | sdbCoA_q2 | sdbCoA_q3 | ssbCCo_q1 | ... | lseCWA_q3 | lteOri_q1 | lteOri_q2 | lteOri_q3 | lteWNB_q1 | lteWNB_q2 | lteWNB_q3 | lieWCe_q1 | lieWCe_q2 | lieWCe_q3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| hindex | |||||||||||||||||||||
| c000e094707t0000 | -0.947406 | -0.371977 | 0.020285 | -0.901199 | -0.237045 | -0.023143 | -0.000419 | -0.001515 | -0.010221 | -0.046170 | ... | 0.073064 | 0.031571 | 0.196520 | 0.424415 | -0.611681 | -0.502087 | -0.311160 | -0.022562 | -0.002733 | -0.004738 |
| c000e094763t0000 | -0.913567 | -0.420861 | -0.271703 | -0.903627 | -0.428003 | -0.336729 | -0.000419 | -0.001515 | -0.010221 | -0.035325 | ... | -0.254395 | -1.016655 | -0.161371 | 0.011093 | 0.148709 | 0.214520 | -0.125943 | -0.019044 | -0.002654 | -0.004738 |
| c000e094763t0001 | -0.878137 | -0.411587 | -0.284021 | -0.900393 | -0.416250 | -0.350010 | -0.000419 | -0.001515 | -0.010221 | -0.034917 | ... | -0.285074 | -0.897625 | -0.161371 | 0.103698 | 0.148709 | 0.250036 | -0.200268 | -0.019323 | -0.002654 | -0.004738 |
| c000e094763t0002 | -0.952475 | -0.421566 | -0.283919 | -0.968400 | -0.429947 | -0.343165 | -0.000419 | -0.001515 | -0.010221 | -0.065649 | ... | -0.280682 | -0.927382 | -0.161371 | 0.177408 | 0.302689 | 0.250036 | -0.120718 | -0.018825 | -0.002654 | -0.004738 |
| c000e094764t0000 | -0.964878 | -0.420861 | -0.271703 | -0.972440 | -0.420006 | -0.315861 | -0.000419 | -0.001515 | -0.010221 | -0.066832 | ... | -0.280682 | -1.016655 | -0.104108 | 0.185348 | 0.302689 | 0.250036 | -0.105044 | -0.018825 | -0.002659 | -0.004738 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| c102e644989t0111 | -0.311466 | -0.431706 | -0.373463 | -0.082269 | -0.459270 | -0.389532 | -0.000419 | -0.001515 | -0.010221 | 0.132837 | ... | 0.199797 | 1.288365 | 0.440493 | 0.197816 | -0.351250 | -0.580453 | -0.704637 | -0.000200 | -0.002667 | -0.004738 |
| c102e644989t0112 | -0.326671 | -0.461825 | -0.371855 | -0.149873 | -0.528701 | -0.386678 | -0.000419 | -0.001515 | -0.010221 | 0.136559 | ... | 0.195101 | 1.288365 | 0.440493 | 0.290197 | -0.351250 | -0.580453 | -0.693005 | -0.000669 | -0.002667 | -0.004738 |
| c102e644989t0113 | -0.094236 | -0.364761 | -0.304254 | 0.024972 | -0.347371 | -0.283669 | -0.000419 | -0.001515 | -0.010221 | 0.021411 | ... | 0.199797 | 1.288365 | 0.440493 | 0.197816 | -0.351250 | -0.580453 | -0.704637 | -0.000843 | -0.002667 | -0.004738 |
| c102e644989t0114 | -0.477667 | -0.568464 | -0.390033 | -0.600170 | -0.646516 | -0.472676 | -0.000419 | -0.001515 | -0.010221 | 0.424887 | ... | 0.008079 | -0.855901 | 0.189420 | -0.560233 | -0.341815 | -0.580453 | -0.704637 | -0.000898 | -0.002667 | -0.004738 |
| c102e644989t0115 | -0.413094 | -0.545952 | -0.382834 | -0.400108 | -0.610332 | -0.440413 | -0.000419 | -0.001515 | -0.010221 | 0.160613 | ... | 0.008079 | -0.203827 | 0.440493 | 0.231812 | -0.351250 | -0.580453 | -0.638809 | -0.000200 | -0.002543 | -0.004738 |
14539578 rows × 177 columns
data = data.replace([np.inf, -np.inf], np.nan).fillna(0)
cgram = Clustergram(range(1, 25), method='minibatchkmeans', batch_size=1_000_000, n_init=100, random_state=42)
cgram.fit(data)
K=1 skipped. Mean computed from data directly.
K=2 fitted in 516.5269868373871 seconds.
K=3 fitted in 568.119576215744 seconds.
K=4 fitted in 630.1900498867035 seconds.
K=5 fitted in 657.8931384086609 seconds.
K=6 fitted in 843.33575963974 seconds.
K=7 fitted in 872.618435382843 seconds.
K=8 fitted in 957.9764461517334 seconds.
K=10 fitted in 1057.0646948814392 seconds.
K=11 fitted in 1112.4249770641327 seconds.
K=13 fitted in 1186.7245635986328 seconds.
K=14 fitted in 1249.940408706665 seconds.
import urbangrammar_graphics as ugg
import seaborn as sns
sns.set(style='whitegrid')
%%time
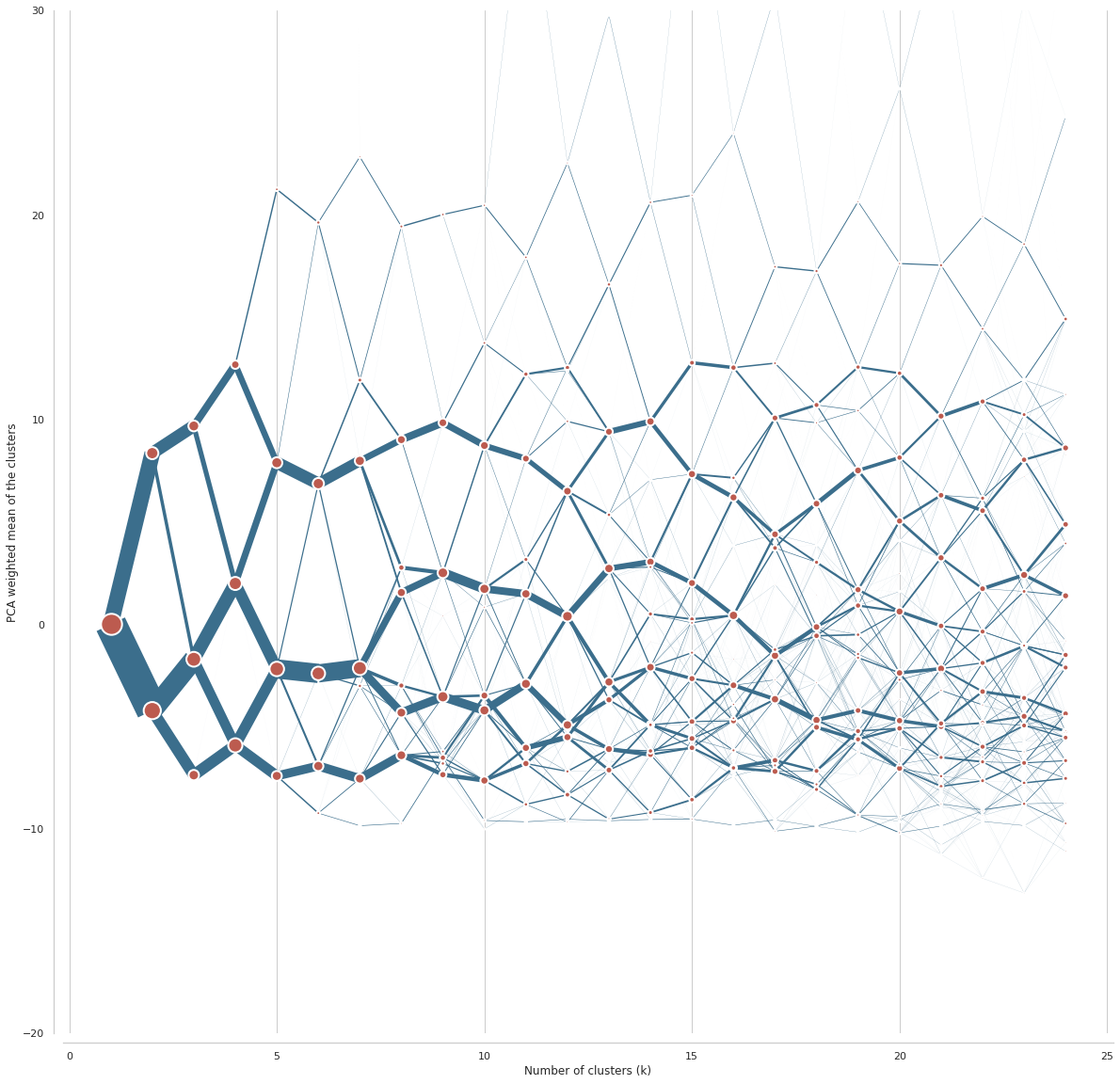
ax = cgram.plot(
figsize=(20, 20),
line_style=dict(color=ugg.COLORS[1]),
cluster_style={"color": ugg.COLORS[2]},
)
ax.yaxis.grid(False)
sns.despine(offset=10)
ax.set_ylim(-20, 30)
CPU times: user 47.3 s, sys: 5.73 s, total: 53.1 s
Wall time: 53 s
(-20.0, 30.0)
from bokeh.io import output_notebook
from bokeh.plotting import show
output_notebook()
fig =MiniBatchKMeansam.bokeh(
figsize=(800, 600),
line_style=dict(color=ugg.HEX[1]),
cluster_style={"color": ugg.HEX[2]},
)
show(fig)
fig2 = cgram.bokeh(
figsize=(800, 600),
line_style=dict(color=ugg.HEX[1]),
cluster_style={"color": ugg.HEX[2]},
pca_weighted=False
)
show(fig2)
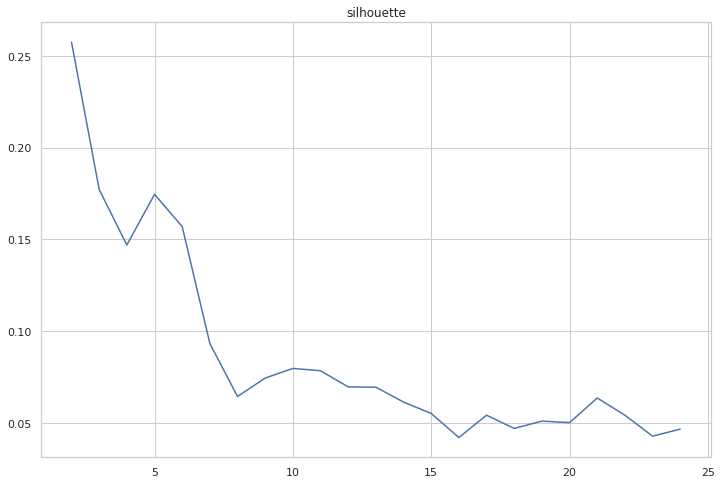
cgram.silhouette_score(sample_size=100_000)
cgram.silhouette.plot(figsize=(12, 8), title="silhouette")
<AxesSubplot:title={'center':'silhouette'}>
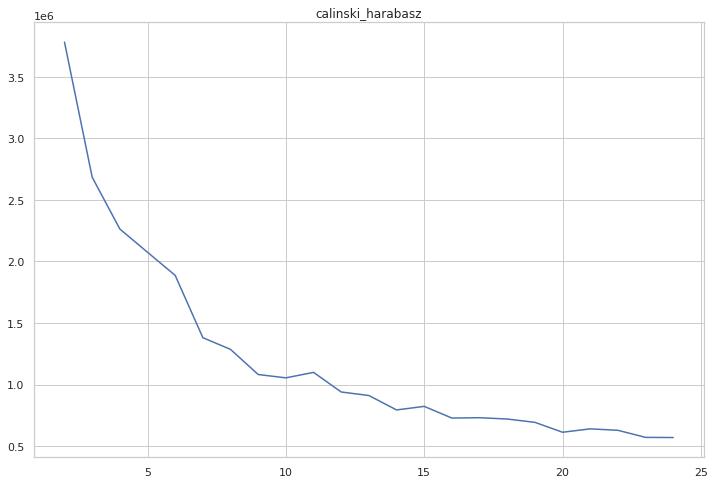
cgram.calinski_harabasz_score()
cgram.calinski_harabasz.plot(figsize=(12, 8), title="calinski_harabasz")
<AxesSubplot:title={'center':'calinski_harabasz'}>
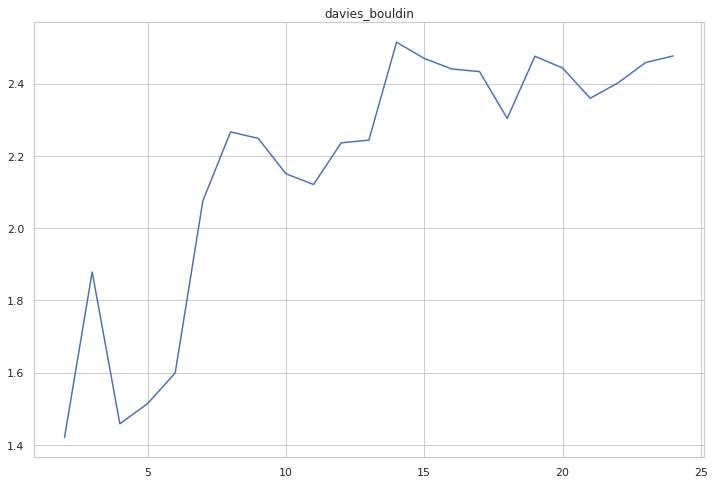
cgram.davies_bouldin_score()
cgram.davies_bouldin.plot(figsize=(12, 8), title="davies_bouldin")
<AxesSubplot:title={'center':'davies_bouldin'}>
labels = cgram.labels.copy()
labels.columns = labels.columns.astype("str")
labels.to_parquet("../../urbangrammar_samba/spatial_signatures/clustering_data/clustergram_form_labels.pq")
import pickle
with open("../../urbangrammar_samba/spatial_signatures/clustering_data/clustergram_form_centers.pickle",'wb') as f:
pickle.dump(cgram.cluster_centers, f)
km = MiniBatchKMeans(n_clusters=8, batch_size=1_000_000, n_init=1000, random_state=42)
%time km.fit(data)
CPU times: user 7h 59min 14s, sys: 6h 38min 22s, total: 14h 37min 37s
Wall time: 2h 27min 42s
MiniBatchKMeans(batch_size=1000000, n_init=1000, random_state=42)
labels = km.labels_
pd.Series(labels).value_counts()
1 5544712
5 3774274
2 3451451
0 1554431
4 151529
3 62701
7 477
6 3
dtype: int64
pd.DataFrame(labels, columns=["k8"], index=data.index).to_parquet("../../urbangrammar_samba/spatial_signatures/clustering_data/k8_form_labels.pq")
Generation of signature geometry¶
With each tessellation cell labelled we now have to dissolve all 14.5 million cells into signature geometry.
import geopandas as gpd
import matplotlib.pyplot as plt
import contextily as ctx
import urbangrammar_graphics as ugg
import dask_geopandas
from utils.dask_geopandas import dask_dissolve
import warnings
warnings.filterwarnings('ignore', message='.*initial implementation of Parquet.*')
labels = pd.read_parquet("../../urbangrammar_samba/spatial_signatures/clustering_data/k8_form_labels.pq")
labels
| k8 | |
|---|---|
| hindex | |
| c000e094707t0000 | 0 |
| c000e094763t0000 | 5 |
| c000e094763t0001 | 5 |
| c000e094763t0002 | 5 |
| c000e094764t0000 | 5 |
| ... | ... |
| c102e644989t0111 | 5 |
| c102e644989t0112 | 5 |
| c102e644989t0113 | 5 |
| c102e644989t0114 | 5 |
| c102e644989t0115 | 5 |
14539578 rows × 1 columns
We first dissolve geometries in each chunk separately and store the result as another parquet file.
for i in range(103):
geom = gpd.read_parquet(f"../../urbangrammar_samba/spatial_signatures/tessellation/tess_{i}.pq", columns=["tessellation", "hindex"]).set_index("hindex")
geom = geom.merge(labels, how="left", left_index=True, right_index=True)
ddf = dask_geopandas.from_geopandas(geom.sort_values('k8'), npartitions=64)
spsig = dask_dissolve(ddf, by='k8').compute().reset_index(drop=True).explode()
spsig.to_parquet(f"../../urbangrammar_samba/spatial_signatures/signatures/temp/spsig_{i}.pq")
print(f"Chunk {i} done.")
Chunk 0 done.
Chunk 1 done.
Chunk 2 done.
Chunk 3 done.
Chunk 4 done.
Chunk 5 done.
Chunk 6 done.
Chunk 7 done.
Chunk 8 done.
Chunk 9 done.
Chunk 10 done.
Chunk 11 done.
Chunk 12 done.
Chunk 13 done.
Chunk 14 done.
Chunk 15 done.
Chunk 16 done.
Chunk 17 done.
Chunk 18 done.
Chunk 19 done.
Chunk 20 done.
Chunk 21 done.
Chunk 22 done.
Chunk 23 done.
Chunk 24 done.
Chunk 25 done.
Chunk 26 done.
Chunk 27 done.
Chunk 28 done.
Chunk 29 done.
Chunk 30 done.
Chunk 31 done.
Chunk 32 done.
Chunk 33 done.
Chunk 34 done.
Chunk 35 done.
Chunk 36 done.
Chunk 37 done.
Chunk 38 done.
Chunk 39 done.
Chunk 40 done.
Chunk 41 done.
Chunk 42 done.
Chunk 43 done.
Chunk 44 done.
Chunk 45 done.
Chunk 46 done.
Chunk 47 done.
Chunk 48 done.
Chunk 49 done.
Chunk 50 done.
Chunk 51 done.
Chunk 52 done.
Chunk 53 done.
Chunk 54 done.
Chunk 55 done.
Chunk 56 done.
Chunk 57 done.
Chunk 58 done.
Chunk 59 done.
Chunk 60 done.
Chunk 61 done.
Chunk 62 done.
Chunk 63 done.
Chunk 64 done.
Chunk 65 done.
Chunk 66 done.
Chunk 67 done.
Chunk 68 done.
Chunk 69 done.
Chunk 70 done.
Chunk 71 done.
Chunk 72 done.
Chunk 73 done.
Chunk 74 done.
Chunk 75 done.
Chunk 76 done.
Chunk 77 done.
Chunk 78 done.
Chunk 79 done.
Chunk 80 done.
Chunk 81 done.
Chunk 82 done.
Chunk 83 done.
Chunk 84 done.
Chunk 85 done.
Chunk 86 done.
Chunk 87 done.
Chunk 88 done.
Chunk 89 done.
Chunk 90 done.
Chunk 91 done.
Chunk 92 done.
Chunk 93 done.
Chunk 94 done.
Chunk 95 done.
Chunk 96 done.
Chunk 97 done.
Chunk 98 done.
Chunk 99 done.
Chunk 100 done.
Chunk 101 done.
Chunk 102 done.
Now we combine all dissolved chunks and dissolve them again to get the final contiguous geometry.
spsigs = pd.concat([gpd.read_parquet(f"../../urbangrammar_samba/spatial_signatures/signatures/temp/spsig_{i}.pq") for i in range(103)])
ddf = dask_geopandas.from_geopandas(spsigs.sort_values('k8').reset_index(drop=True), npartitions=64)
spsig = dask_dissolve(ddf, by='k8').compute().reset_index(drop=True).explode()
spsig.to_parquet(f"../../urbangrammar_samba/spatial_signatures/signatures/signatures_form_K8_GB.pq")
spsig
| k8 | tessellation | ||
|---|---|---|---|
| 0 | 0 | 0 | POLYGON Z ((89280.000 7920.000 0.000, 89190.00... |
| 1 | 0 | POLYGON Z ((92602.729 11420.758 0.000, 92581.2... | |
| 2 | 0 | POLYGON Z ((169705.076 15498.752 0.000, 169706... | |
| 3 | 0 | POLYGON Z ((170058.697 15486.278 0.000, 170003... | |
| 4 | 0 | POLYGON Z ((169696.219 16164.689 0.000, 169694... | |
| ... | ... | ... | ... |
| 7 | 5 | 7 | POLYGON Z ((293374.200 758731.000 0.000, 29335... |
| 6 | 7 | POLYGON Z ((283647.720 803019.800 0.000, 28364... | |
| 7 | 7 | POLYGON Z ((285459.203 803844.804 0.000, 28545... | |
| 8 | 7 | POLYGON Z ((283841.987 803707.777 0.000, 28384... | |
| 9 | 7 | POLYGON Z ((290570.716 809730.511 0.000, 29056... |
52393 rows × 2 columns
The resulting geometry is dense and complicated. For exploration purposes, it is better to simplify it.
ddf = dask_geopandas.from_geopandas(spsig.reset_index().rename_geometry("geometry"), npartitions=64)
ddf.geometry = ddf.simplify(2).buffer(.001).simplify(2)
%time spsig = ddf.compute()
CPU times: user 27min 16s, sys: 6min 23s, total: 33min 40s
Wall time: 27min 11s
Now we save our geometries to files.
spsig.to_file(f"../../urbangrammar_samba/spatial_signatures/signatures/signatures_form_K8_GB_simplified.geojson", driver="GeoJSON")
spsig.to_parquet(f"../../urbangrammar_samba/spatial_signatures/signatures/signatures_form_K8_GB_simplified.pq")